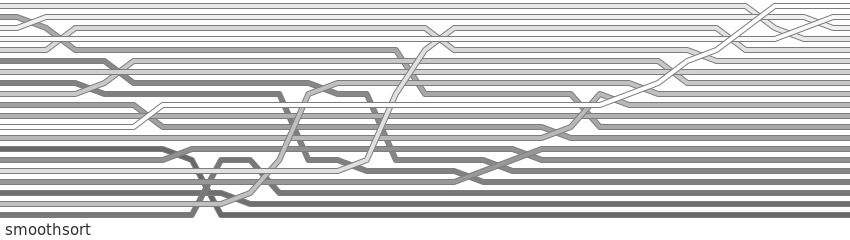
smoothsort

code

# Possibly replace with a generator that produces Leonardo numbers?
# That would be of limited utility since this is all of them up to 31 bits.
LP = [ 1, 1, 3, 5, 9, 15, 25, 41, 67, 109, 177, 287, 465, 753, 1219, 1973,
       3193, 5167, 8361, 13529, 21891, 35421, 57313, 92735, 150049, 242785,
       392835, 635621, 1028457, 1664079, 2692537, 4356617, 7049155,
       11405773, 18454929, 29860703, 48315633, 78176337, 126491971,
       204668309, 331160281, 535828591, 866988873 ]

# Solution for determining number of trailing zeroes of a number's binary representation.
# Taken from http://www.0xe3.com/text/ntz/ComputingTrailingZerosHOWTO.html
# I don't much like the magic numbers, but they really are magic.
MultiplyDeBruijnBitPosition = [ 0,  1, 28,  2, 29, 14, 24, 3,
                                30, 22, 20, 15, 25, 17,  4, 8,
                                31, 27, 13, 23, 21, 19, 16, 7,
                                26, 12, 18,  6, 11,  5, 10, 9]

def trailingzeroes(v):
    return MultiplyDeBruijnBitPosition[(((v & -v) * 0x077CB531) >> 27) & 0b11111]


def sift(lst, pshift, head):
    while pshift > 1:
        rt = head - 1
        lf = head - 1 - LP[pshift - 2]
        if lst[head] >= lst[lf] and lst[head] >= lst[rt]:
            break
        if lst[lf] >= lst[rt]:
            lst[head], lst[lf] = lst[lf], lst[head]
            head = lf
            pshift -= 1
        else:
            lst[head], lst[rt] = lst[rt], lst[head]
            head = rt
            pshift -= 2
        lst.log()


def trinkle(lst, p, pshift, head, trusty):
    while p != 1:
        stepson = head - LP[pshift]
        if lst[stepson] <= lst[head]:
            break
        if not trusty and pshift > 1:
            rt = head - 1
            lf = head - 1 - LP[pshift - 2]
            if lst[rt] >= lst[stepson] or lst[lf] >= lst[stepson]:
                break
        lst[head], lst[stepson] = lst[stepson], lst[head]
        lst.log()
        head = stepson
        trail = trailingzeroes(p & ~1)
        p >>= trail
        pshift += trail
        trusty = False

    if not trusty:
        sift(lst, pshift, head)


def smoothsort(lst):
    p = 1
    pshift = 1
    head = 0
    while head < len(lst) - 1:
        if (p & 3) == 3:
            sift(lst, pshift, head)
            p >>= 2
            pshift += 2
        else:
            if LP[pshift - 1] >= len(lst) - 1 - head:
                trinkle(lst, p, pshift, head, False)
            else:
                sift(lst, pshift, head)

            if pshift == 1:
                p <<= 1
                pshift -= 1
            else:
                p <<= pshift - 1
                pshift = 1

        p |= 1
        head += 1
    trinkle(lst, p, pshift, head, False)
    while pshift != 1 or p != 1:
        if pshift <= 1:
            trail = trailingzeroes(p & ~1)
            p >>= trail
            pshift += trail
        else:
            p <<= 2
            p ^= 7
            pshift -= 2

            trinkle(lst, p >> 1, pshift + 1, head - LP[pshift] - 1, True)
            trinkle(lst, p, pshift, head - 1, True)
        head -= 1

List order is sampled for visualisation whenever lst.log() is called.